Summaries A lonely woman befriends a group of teenagers and decides to let them party at her house. Just when the kids think their luck couldn't get any better, things start happening that make them question the intention of their host. Third and fourth graders learn about basic reading concepts including the various parts of plot, as well as characters and setting. Parents and students can work together at home to reinforce what a child learns in school. Read on to learn more about identifying characters, determining the setting, and understanding the plot of a book or story. The Moving Average is a popular indicator used by forex traders to identify trends. Learn how to use and interpret moving averages in technical analysis. An MA-plot is a plot of log-intensity ratios (M-values) versus log-intensity averages (A-values). See Ritchie et al (2015) for a brief historical review. For two color data objects, a within-array MA-plot is produced with the M and A values computed from the two channels for the specified array. The second plot is acf with ci.type='ma': The persistence of high values in acf plot probably represent a long term positive trend. The question is if this represent seasonal variation? I tried to see different sites on this topic but I am not sure if these plots show seasonality. ACF and PACF plot analysis. Help interpreting ACF- and PACF-plots.
- Ma Plots Explanation Example
- Ma Plots Explanation 3
- Ma Plots Explanation Worksheet
- Ma Plots Explanation Definition
- Ma Plots Explanation Definition
- Ma Plots Explanation Meaning
- Ma Plots Explanation 2
Update
I've rewritten this blog post elsewhere, so you may want to read that version instead (I think it's much better than this one)
In this post, we'll talk about the method for explaining the predictions of any classifier described in this paper, and implemented in this open source package.
Motivation: why do we want to understand predictions?
Machine learning is a buzzword these days. With computers beating professionals in games like Go, many people have started asking if machines would also make for better drivers, or even doctors.
Many of the state of the art machine learning models are functionally black boxes, as it is nearly impossible to get a feeling for its inner workings. This brings us to a question of trust: do I trust that a certain prediction from the model is correct? Or do I even trust that the model is making reasonable predictions in general?While the stakes are low in a Go game, they are much higher if a computer is replacing my doctor, or deciding if I am a suspect of terrorism (Person of Interest, anyone?). Perhaps more commonly, if a company is replacing some system with one based on machine learning, it has to trust that the machine learning model will behave reasonably well.
It seems intuitive that explaining the rationale behind individual predictions would make us better positioned to trust or mistrust the prediction, or the classifier as a whole. Even if we can't necessarily understand how the model behaves on all cases, it may be possible (and indeed it is in most cases) to understand how it behaves in particular cases.
Ma Plots Explanation Example
Finally, a word on accuracy. If you have had experience with machine learning, I bet you are thinking something along the lines of: 'of course I know my model is going to perform well in the real world, I have really high cross validation accuracy! Why do I need to understand it's predictions when I know it gets it right 99% of the time?'. As anyone who has used machine learning in the real world (not only in a static dataset) can attest, accuracy on cross validation can be very misleading. Sometimes data that shouldn't be available leaks into the training data accidentaly. Sometimes the way you gather data introduces correlations that will not exist in the real world, which the model exploits. Many other tricky problems can give us a false understanding of performance, even in doing A/B tests. I am not saying you shouldn't measure accuracy, but simply that it should not be your only metric for assessing trust.
Lime: A couple of examples.
Can you really trust your 20 newsgroups classifier?
First, we give an example from text classification. The famous 20 newsgroups dataset is a benchmark in the field, and has been used to compare different models in several papers. We take two classes that are suposedly harder to distinguish, due to the fact that they share many words: Christianity and Atheism. Training a random forest with 500 trees, we get a test set accuracy of 92.4%, which is surprisingly high. If accuracy was our only measure of trust, we would definitely trust this algorithm.
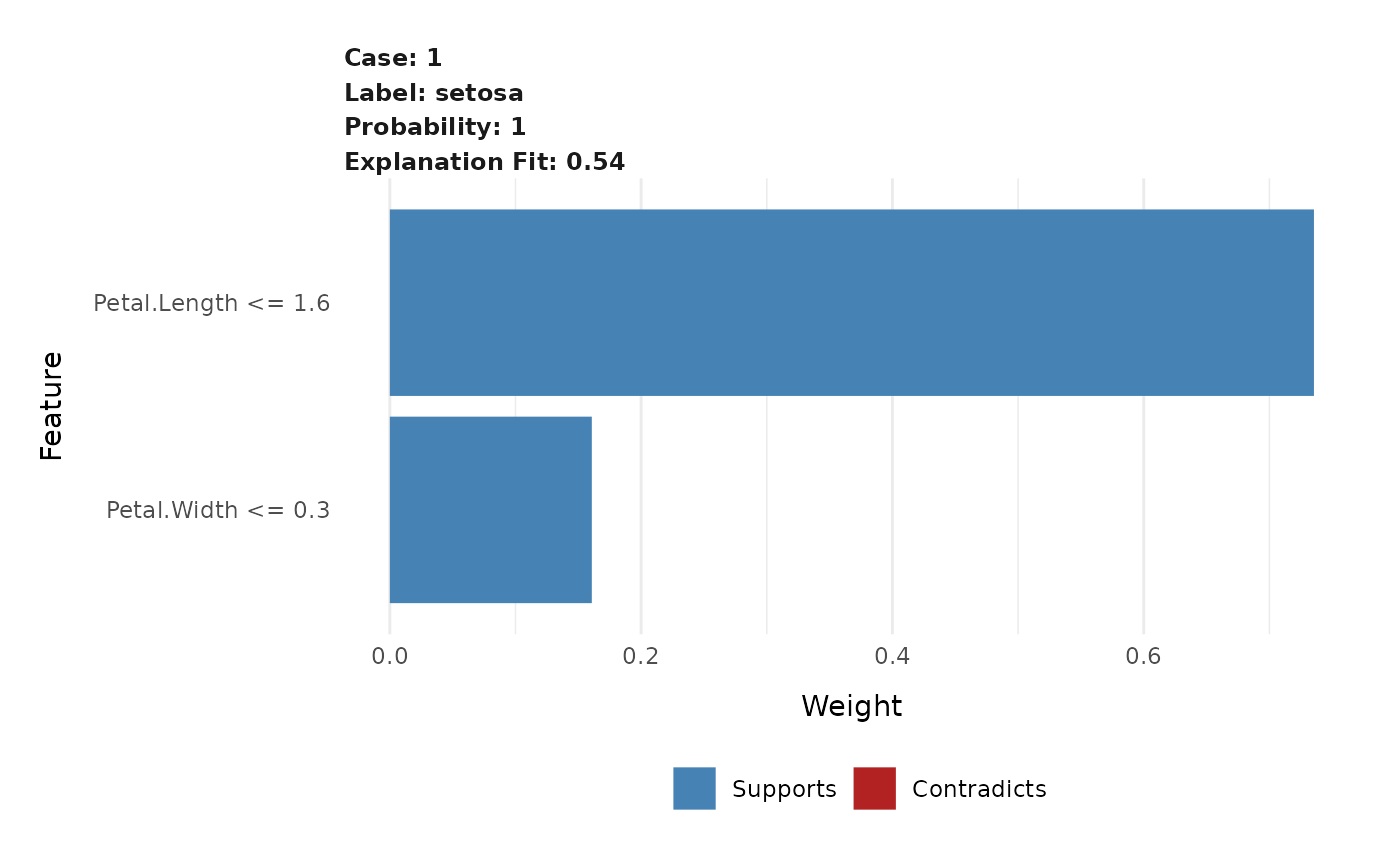
Below is an explanation for an arbitrary instance in the test set, generated using the lime package.
This is a case where the classifier predicts the instance correctly, but for the wrong reasons. A little further exploration shows us that the word 'Posting' (part of the email header) appears in 21.6% of the examples in the training set, only two times in the class 'Christianity'. This is repeated on the test set, where it appears in almost 20% of the examples, only twice in 'Christianity'. This kind of quirk in the dataset makes the problem much easier than it is in the real world, where this classifier would not be able to distinguish between christianity and atheism documents. This is hard to see just by looking at accuracy or raw data, but easy once explanations are provided. Such insights become common once you understand what models are actually doing, leading to models that generalize much better.
Note further how interpretable the explanations are: they correspond to a very sparse linear model (with only 6 features). Even though the underlying classifier is a complicated random forest, in the neighborhood of this example it behaves roughly as a linear model. Sure enough, if we remove the words 'Host' and 'NNTP' from the example, the 'atheism' prediction probability becomes close to 0.57 - 0.14 - 0.12 = 0.31.
Explaining predictions from a Deep Neural Network
Below is an image from our paper, where we explain Google's Inception neural network on some arbitary images. In this case, we keep as explanations the parts of the image that are most positive towards a certain class. In this case, the classifier predicts Electric Guitar even though the image contains an acoustic guitar. The explanation reveals why it would confuse the two: the fretboard is very similar. Getting explanations for image classifiers is something that is not yet available in the lime package, but we are working on it.
Lime: how we get explanations
Lime is short for Local Interpretable Model-Agnostic Explanations. Each part of the name reflects something that we desire in explanations. Local refers to local fidelity - i.e., we want the explanation to really reflect the behaviour of the classifier 'around' the instance being predicted. This explanation is useless unless it is interpretable - that is, unless a human can make sense of it. Lime is able to explain any model without needing to 'peak' into it, so it is model-agnostic. We now give a high level overview of how lime works. For more details, check out our paper.
First, a word about interpretability. Some classifiers use representations that are not intuitive to users at all (e.g. word embeddings). Lime explains those classifiers in terms of interpretable representations (words), even if that is not the representation actually used by the classifier. Further, lime takes human limitations into account: i.e. the explanations are not too long. Right now, our package supports explanations that are sparse linear models (as presented before), although we are working on other representations.
In order to be model-agnostic, lime can't peak into the model. In order to figure out what parts of the interpretable input are contributing to the prediction, we perturb the input around its neighborhood and see how the model's predictions behave. We then weight these perturbed data points by their proximity to the original example, and learn an interpretable model on those and the associated predictions. For example, if we are trying to explain the prediction for the sentence 'I hate this movie', we will perturb the sentence and get predictions on sentences such as 'I hate movie', 'I this movie', 'I movie', 'I hate', etc. Even if the original classifier takes many more words into account globally, it is reasonable to expect that around this example only the word 'hate' will be relevant. Note that if the classifier uses some uninterpretable representation such as word embeddings, this still works: we just represent the perturbed sentences with word embeddings, and the explanation will still be in terms of words such as 'hate' or 'movie'.
An illustration of this process is given below. The original model's decision function is represented by the blue/pink background, and is clearly nonlinear.The bright red cross is the instance being explained (let's call it X).We sample perturbed instances around X, and weight them according to their proximity to X (weight here is represented by size). We get original model's prediction on these perturbed instances, and then learn a linear model (dashed line) that approximates the model well in the vicinity of X. Note that the explanation in this case is not faithful globally, but it is faithful locally around X.
Conclusion
I hope I've convinced you that understanding individual predictions from classifiers is an important problem. Having explanations lets you make an informed decision about how much you trust the prediction or the model as a whole, and provides insights that can be used to improve the model.
Links to code and paper (again)
If you're interested in going more in-depth into how lime works, and the kinds of experiments we did to validate the usefulness of such explanations, here is a link to pre-print paper.
If you are interested in trying lime for text classifiers, make sure you check out our python package. Installation is as simple as typing:
Ma Plots Explanation 3
pip install lime
The package is very easy to use. It is particulary easy to explain scikit-learn classifiers. In the github page we also link to a few tutorials, such as this one, with examples from scikit-learn.
In the previous set of articles (Parts 1, 2 and 3) we went into significant detail about the AR(p), MA(q) and ARMA(p,q) linear time series models. We used these models to generate simulated data sets, fitted models to recover parameters and then applied these models to financial equities data.
In this article we are going to discuss an extension of the ARMA model, namely the Autoregressive Integrated Moving Average model, or ARIMA(p,d,q) model. We will see that it is necessary to consider the ARIMA model when we have non-stationary series. Such series occur in the presence of stochastic trends.
Quick Recap and Next Steps
To date we have considered the following models (the links will take you to the appropriate articles):
We have steadily built up our understanding of time series with concepts such as serial correlation, stationarity, linearity, residuals, correlograms, simulating, fitting, seasonality, conditional heteroscedasticity and hypothesis testing.
As of yet we have not carried out any prediction or forecasting from our models and so have not had any mechanism for producing a trading system or equity curve.
Once we have studied ARIMA (in this article), ARCH and GARCH (in the next articles), we will be in a position to build a basic long-term trading strategy based on prediction of stock market index returns.
Despite the fact that I have gone into a lot of detail about models which we know will ultimately not have great performance (AR, MA, ARMA), we are now well-versed in the process of time series modeling.
This means that when we come to study more recent models (and even those currently in the research literature), we will have a significant knowledge base on which to draw, in order to effectively evaluate these models, instead of treating them as a 'turn key' prescription or 'black box'.
More importantly, it will provide us with the confidence to extend and modify them on our own and understand what we are doing when we do it!
I'd like to thank you for being patient so far, as it might seem that these articles are far away from the 'real action' of actual trading. However, true quantitative trading research is careful, measured and takes significant time to get right. There is no quick fix or 'get rich scheme' in quant trading.
We're very nearly ready to consider our first trading model, which will be a mixture of ARIMA and GARCH, so it is imperative that we spend some time understanding the ARIMA model well!
Once we have built our first trading model, we are going to consider more advanced models such as long-memory processes, state-space models (i.e. the Kalman Filter) and Vector Autoregressive (VAR) models, which will lead us to other, more sophisticated, trading strategies.
Autoregressive Integrated Moving Average (ARIMA) Models of order p, d, q
Rationale
ARIMA models are used because they can reduce a non-stationary series to a stationary series using a sequence of differencing steps.

We can recall from the article on white noise and random walks that if we apply the difference operator to a random walk series ${x_t }$ (a non-stationary series) we are left with white noise ${w_t }$ (a stationary series):
begin{eqnarray} nabla x_t = x_t - x_{t-1} = w_t end{eqnarray}ARIMA essentially performs this function, but does so repeatedly, $d$ times, in order to reduce a non-stationary series to a stationary one.
In order to handle other forms of non-stationarity beyond stochastic trends additional models can be used.
Seasonality effects (such as those that occur in commodity prices) can be tackled with the Seasonal ARIMA model (SARIMA), however we won't be discussing SARIMA much in this series.
Conditional heteroscedastic effects (as with volatility clustering in equities indexes) can be tackled with ARCH/GARCH.
In this article we will be considering non-stationary series with stochastic trends and fit ARIMA models to these series. We will also finally produce forecasts for our financial series.
Definitions
Prior to defining ARIMA processes we need to discuss the concept of an integrated series:
Integrated Series of order $d$
A time series ${ x_t }$ is integrated of order $d$, $I(d)$, if:
begin{eqnarray} nabla^d x_t = w_t end{eqnarray}That is, if we difference the series $d$ times we receive a discrete white noise series.
Alternatively, using the Backward Shift Operator ${bf B}$ an equivalent condition is:
begin{eqnarray} (1-{bf B}^d) x_t = w_t end{eqnarray}Now that we have defined an integrated series we can define the ARIMA process itself:
Autoregressive Integrated Moving Average Model of order p, d, q
A time series ${x_t }$ is an autoregressive integrated moving average model of order p, d, q, ARIMA(p,d,q), if $nabla^d x_t$ is an autoregressive moving average of order p,q, ARMA(p,q).
That is, if the series ${x_t }$ is differenced $d$ times, and it then follows an ARMA(p,q) process, then it is an ARIMA(p,d,q) series.
If we use the polynomial notation from Part 1 and Part 2 of the ARMA series, then an ARIMA(p,d,q) process can be written in terms of the Backward Shift Operator, ${bf B}$:
begin{eqnarray} theta_p({bf B})(1-{bf B})^d x_t = phi_q ({bf B}) w_t end{eqnarray}Ma Plots Explanation Worksheet
Where $w_t$ is a discrete white noise series.

There are some points to note about these definitions.
Since the random walk is given by $x_t = x_{t-1} + w_t$ it can be seen that $I(1)$ is another representation, since $nabla^1 x_t = w_t$.
If we suspect a non-linear trend then we might be able to use repeated differencing (i.e. $d > 1$) to reduce a series to stationary white noise.
In R we can use the diff command with additional parameters, e.g. diff(x, d=3) to carry out repeated differences.
Simulation, Correlogram and Model Fitting
Since we have already made use of the arima.sim command to simulate an ARMA(p,q) process, the following procedure will be similar to that carried out in Part 3 of the ARMA series.
The major difference is that we will now set $d=1$, that is, we will produce a non-stationary time series with a stochastic trending component.
As before we will fit an ARIMA model to our simulated data, attempt to recover the parameters, create confidence intervals for these parameters, produce a correlogram of the residuals of the fitted model and finally carry out a Ljung-Box test to establish whether we have a good fit.
We are going to simulate an ARIMA(1,1,1) model, with the autoregressive coefficient $alpha=0.6$ and the moving average coefficient $beta=-0.5$. Here is the R code to simulate and plot such a series:
Plot of simulated ARIMA(1,1,1) model with $alpha=0.6$ and $beta=-0.5$
Now that we have our simulated series we are going to try and fit an ARIMA(1,1,1) model to it. Since we know the order we will simply specify it in the fit:
The confidence intervals are calculated as:
Both parameter estimates fall within the confidence intervals and are close to the true parameter values of the simulated ARIMA series. Hence, we shouldn't be surprised to see the residuals looking like a realisation of discrete white noise:
Correlogram of the residuals of the fitted ARIMA(1,1,1) model
Finally, we can run a Ljung-Box test to provide statistical evidence of a good fit:
We can see that the p-value is significantly larger than 0.05 and as such we can state that there is strong evidence for discrete white noise being a good fit to the residuals. Hence, the ARIMA(1,1,1) model is a good fit, as expected.
Financial Data and Prediction
In this section we are going to fit ARIMA models to Amazon, Inc. (AMZN) and the S&P500 US Equity Index (^GPSC, in Yahoo Finance). We will make use of the forecast library, written by Rob J Hyndman.
Let's go ahead and install the library in R:
Now we can use quantmod to download the daily price series of Amazon from the start of 2013. Since we will have already taken the first order differences of the series, the ARIMA fit carried out shortly will not require $d > 0$ for the integrated component:
As in Part 3 of the ARMA series, we are now going to loop through the combinations of $p$, $d$ and $q$, to find the optimal ARIMA(p,d,q) model. By 'optimal' we mean the order combination that minimises the Akaike Information Criterion (AIC):
We can see that an order of $p=4$, $d=0$, $q=4$ was selected. Notably $d=0$, as we have already taken first order differences above:
If we plot the correlogram of the residuals we can see if we have evidence for a discrete white noise series:
Correlogram of residuals of ARIMA(4,0,4) model fitted to AMZN daily log returns
There are two significant peaks, namely at $k=15$ and $k=21$, although we should expect to see statistically significant peaks simply due to sampling variation 5% of the time. Let's perform a Ljung-Box test (see previous article) and see if we have evidence for a good fit:
As we can see the p-value is greater than 0.05 and so we have evidence for a good fit at the 95% level.
We can now use the forecast command from the forecast library in order to predict 25 days ahead for the returns series of Amazon:
25-day forecast of AMZN daily log returns
We can see the point forecasts for the next 25 days with 95% (dark blue) and 99% (light blue) error bands. We will be using these forecasts in our first time series trading strategy when we come to combine ARIMA and GARCH.
Let's carry out the same procedure for the S&P500. Firstly we obtain the data from quantmod and convert it to a daily log returns stream:
We fit an ARIMA model by looping over the values of p, d and q:
Ma Plots Explanation Definition
The AIC tells us that the 'best' model is the ARIMA(2,0,1) model. Notice once again that $d=0$, as we have already taken first order differences of the series:
We can plot the residuals of the fitted model to see if we have evidence of discrete white noise:
Correlogram of residuals of ARIMA(2,0,1) model fitted to S&P500 daily log returns
The correlogram looks promising, so the next step is to run the Ljung-Box test and confirm that we have a good model fit:
Since the p-value is greater than 0.05 we have evidence of a good model fit.
Why is it that in the previous article our Ljung-Box test for the S&P500 showed that the ARMA(3,3) was a poor fit for the daily log returns?
Notice that I deliberately truncated the S&P500 data to start from 2013 onwards in this article, which conveniently excludes the volatile periods around 2007-2008. Hence we have excluded a large portion of the S&P500 where we had excessive volatility clustering. This impacts the serial correlation of the series and hence has the effect of making the series seem 'more stationary' than it has been in the past.
This is a very important point. When analysing time series we need to be extremely careful of conditionally heteroscedastic series, such as stock market indexes. In quantitative finance, trying to determine periods of differing volatility is often known as 'regime detection'. It is one of the harder tasks to achieve!
We'll discuss this point at length in the next article when we come to consider the ARCH and GARCH models.
Let's now plot a forecast for the next 25 days of the S&P500 daily log returns:
25-day forecast of S&P500 daily log returns
Now that we have the ability to fit and forecast models such as ARIMA, we're very close to being able to create strategy indicators for trading.
Ma Plots Explanation Definition
Next Steps
Ma Plots Explanation Meaning
In the next article we are going to take a look at the Generalised Autoregressive Conditional Heteroscedasticity (GARCH) model and use it to explain more of the serial correlation in certain equities and equity index series.
Ma Plots Explanation 2
Once we have discussed GARCH we will be in a position to combine it with the ARIMA model and create signal indicators and thus a basic quantitative trading strategy.
